728x90
반응형
[ 백준 11729번. 하노이 탑 이동순서 ]
- 문제명 : 하노이 탑 이동순서
- 사용언어 : python
- 알고리즘 : 재귀
문제
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.
1. 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
2. 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.
아래 그림은 원판이 5개인 경우의 예시이다.
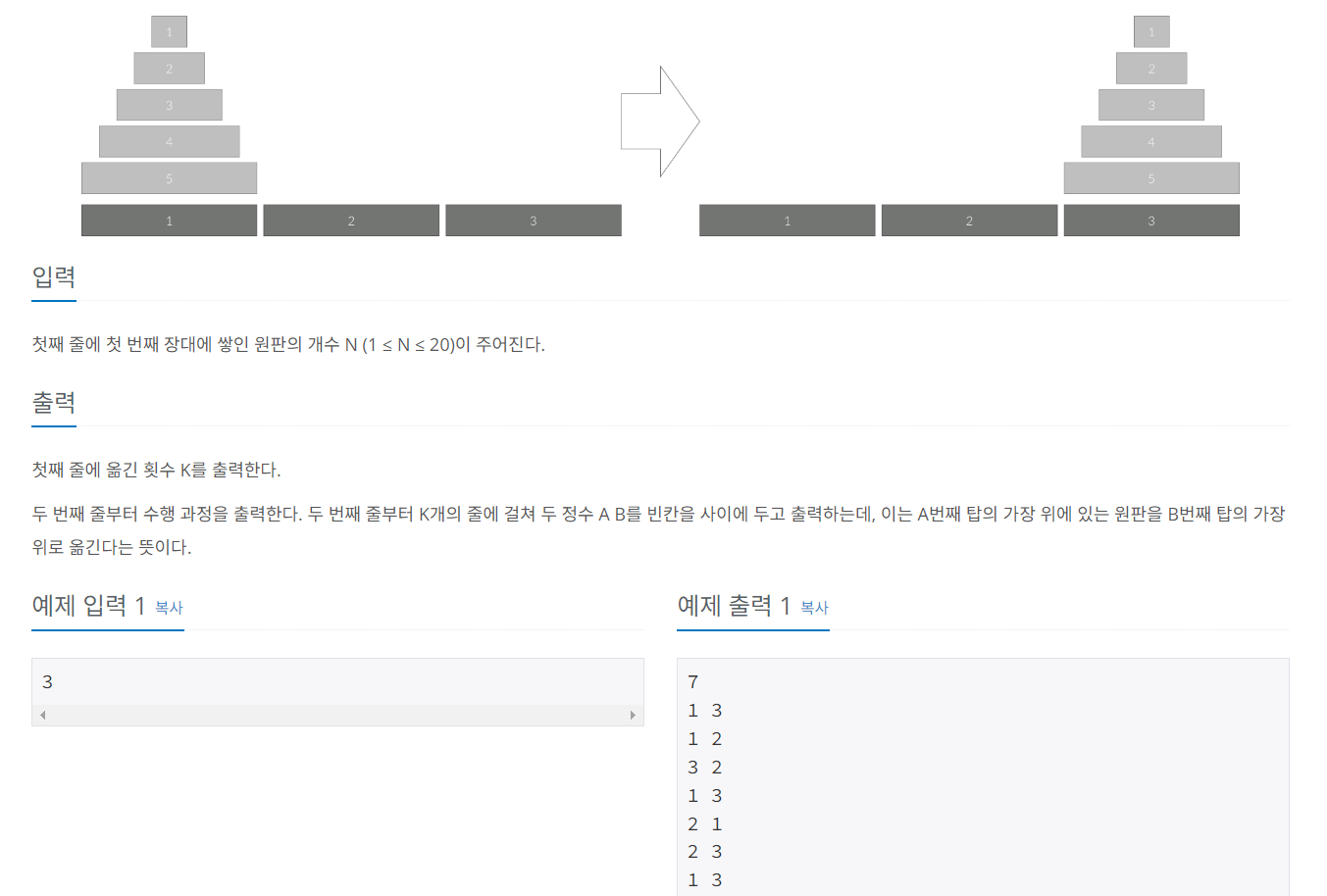
알고리즘 및 실행 코드
'하노이 탑'은 재귀를 이해하기의 대표적인 문제이다.
▽ 재귀의 핵심 정리
1. 재귀는 트리의 형태로 표현. 어떤 방식으로 순회할지를 생각해서 코드 짜기 !
2. 재귀는 자기보다 작은 규모의 문제를 먼저 해결하고 그것을 자기의 문제에 이용하는 것.
3. Base Case + Recursive Case
재귀는 이해가 가도 '하노이 탑'을 이해해도 알고리즘을 바로 떠오르는 것이 쉽지 않았다.
그래서 예시로 원반이 2개, 3개일 때를 하나씩 세어보면서 패턴을 이해하였다.
하노이 탑에서는 원반개수와 기둥 3개가 중요하다. 기둥 3개는 각 시작, 보조, 목표인 것을 잘 생각해야 된다.

▽ 실행 코드
work = []
def move(start, end):
move = start + " " + end
work.append(move)
def hanoi(N, start, end, sub):
if N == 1:
move(start, end)
return
else :
hanoi(N-1, start, sub, end)
move(start, end)
hanoi(N-1, sub, end, start)
N = int(input())
hanoi(N, '1', '3', '2')
print(len(work))
for i in range(len(work)):
print(work[i])
결과

728x90
반응형
'Algorithm' 카테고리의 다른 글
| [Algorithm] Softeer [21년 재직자 대회 예선] 회의실 예약 (python) (1) | 2024.02.02 |
|---|---|
| [Algorithm] Softeer [21년 재직자 대회 예선] 좌석관리 (python) (1) | 2024.02.01 |
| [Algorithm] BAEKJOON 10026번. 적록색약 (python) (0) | 2024.01.26 |
| [Algorithm] Softeer 장애물 인식 프로그램 (Python) (0) | 2024.01.24 |
| [Algorithm] Softeer 조립라인 - Lv.3 (Python) (0) | 2024.01.23 |


댓글